Abraham de Moivre
(26 May 1667 – 27 November 1754) was a French mathematician known for de Moivre's formula, one of those that link complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton,Edmond Halley, and James Stirling. Among his fellow Huguenot exiles in England, he was a colleague of the editor and translator Pierre des Maizeaux.
De Moivre wrote a book on probability theory, The Doctrine of Chances, said to have been prized by gamblers. De Moivre first discovered Binet's formula, the closed-form expression for Fibonacci numbers linking the nth power of the golden ratio φ to the nth Fibonacci number.
De Moivre's Formula
In 1707 de Moivre derived:
which he was able to prove for all positive odd numbers n.[12] In 1722 he suggested it in the more well known form of de Moivre's Formula:
In 1749 Euler proved this formula for any real n using Euler's formula, which makes the proof quite straightforward. This formula is important because it relates complex numbersand trigonometry. Additionally, this formula allows the derivation of useful expressions for cos(nx) and sin(nx) in terms of cos(x) and sin(x).

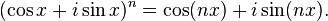
No comments:
Post a Comment